Hessian Matrix

Hessian Matrix : 어떠한 함수의 이계도함수를 행렬로 표현한것 / 이계도함수가 연속이라면 Hessian Matrix은 Symmetric Matrix

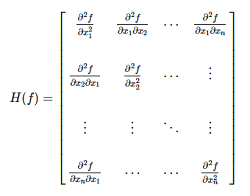
아래의 그림은 실함수 $f(x_1,x_2,x_3,…,x_n)$에 대하여 Hessian Matrix를 나타낸것이다.
=> 함수 $f$의 이계도함수를 이용하여 행렬을 만든것이다.

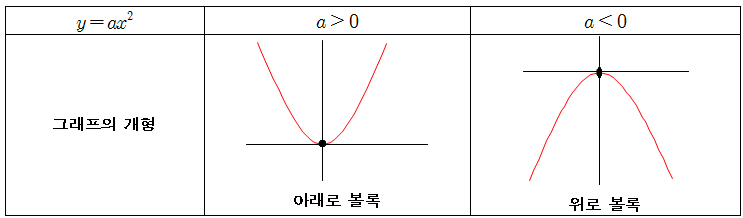
우리는 보통 미분을 이용하여 함수의 기울기, 변곡점을 찾는다. 즉, 함수의 형태를 파악한다. 2차함수의 경우 이계도함수를 통해 +면 아래로 볼록, -면 위로 볼록이라는 것을 알 수 있었다.

이와 마찬가지로 다변수 함수에서는 Hessian Matrix(이계도함수의 Matrix) 이용하여 함수의 형태를 파악한다.

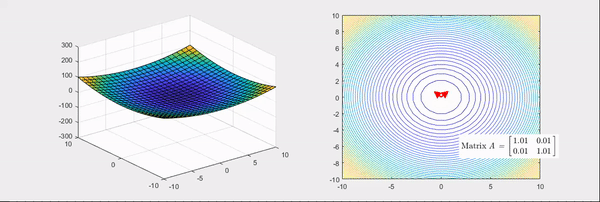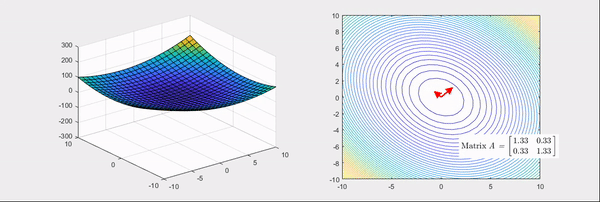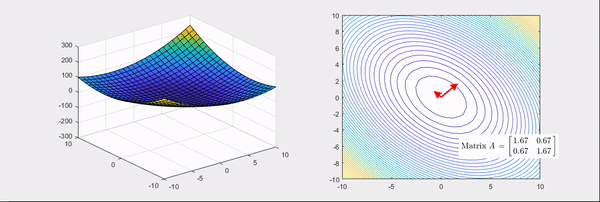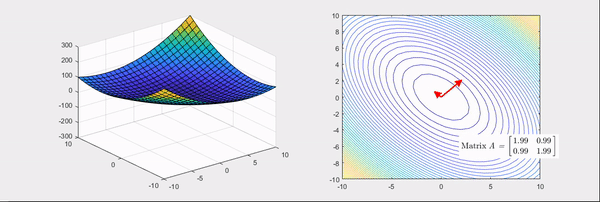
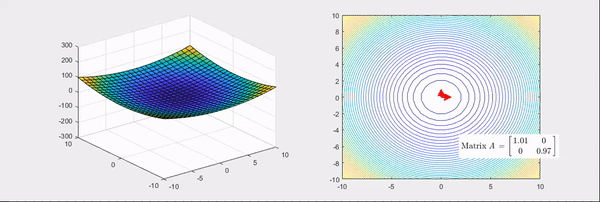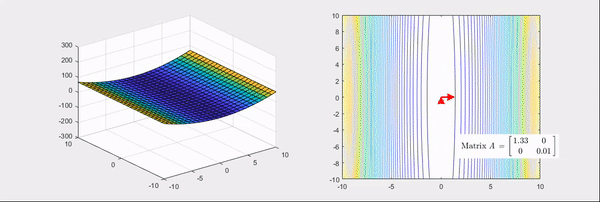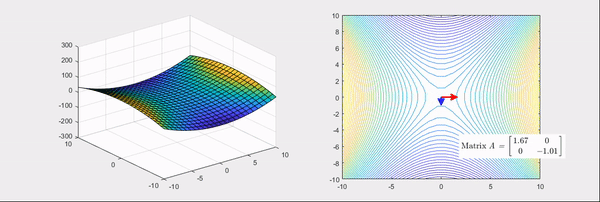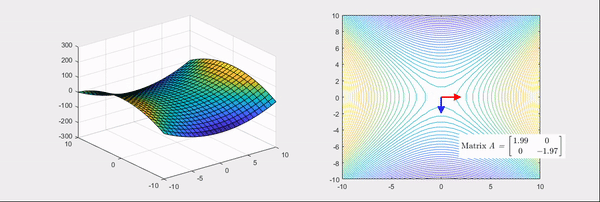
Eigenvector : 화살표 방향 / Eigenvalue : 화살표 크기, (빨간색: 양수 / 파란색: 음수)

Hessian Matrix은 위의 그림과 같이 bowl형태의 함수를 변환시킨다.

Hessian Matrix의 성질을 알아보면, Eigenvalue에 따라 함수의 그래프가 변환된다.
모두 + => 위로 볼록
모두 - => 아래로 볼록
+, - => 안장점

조금 더 자세히 알아보면, Matrix는 어떠한 공간의 선형 변환이라고 볼 수 있다.
예를들어 회전변환 / 위치변환 / 크기변환 모두 Matrix에 의한 변형이라고 볼수있다.

Hessian Matrix도 공간의 변형을 일으킨다. Hessian Matrix의 Eigenvector와 Eigenvalue에 따라 변형을 일으킨다.

위에서 말했듯이, 이계도함수가 연속이라면 Hessian Matrix는 Symmetric Matrix이고, Symmetric Matrix면 Eigenvector는 직각을 이루며, Eigenvalue는 실수의 고유값을 갖는다.

그렇기 때문에 Eigenvector가 Main Axis, Eigenvalue가 Scale이라는 기준이 되어 함수를 변형시키게 된다.